专业预测：湖北以外的疫情何时结束？

目前，新型冠状病毒感染导致的肺炎（以下简称新冠肺炎）的新增确诊病例数量连续几日持续下降，疫情防控措施已经起到明显的效果。除了湖北地区的疫情依然严峻之外，全国其他省市总体明显好转。2月12日我们《专业模型预测，新型肺炎疫情拐点何时来临？》文章中重点分析了全国包括湖北在内的总体疫情的拐点，工业界许多朋友都非常关心湖北外的疫情何时结束并恢复正常的生产秩序，希望我们再写一篇针对全国不含湖北地区的疫情分析预测。

话不多说，我们先上结论：截至2020年2月16日24:00，全国（不含湖北及港澳台地区）新冠肺炎现有确诊病例数量峰值已经过去，即将进入加速减少阶段，新增确诊病例数将在2月19日左右降至个位数，确诊病例在4月8日左右降至个位数，4月中下旬疫情结束。

想了解详细建模过程的请往下阅读。

1、疫情数据准备

注：疫情数据全部来自国家卫生健康委员会及湖北省卫生健康委员会官方网站。

我们使用了从2020年2月1日开始至2020年2月13日这段时间的数据用于疫情传播动力学模型的参数辨识，2月14日至15日的数据用于检验模型效果。

数据集组成：

全国（不含湖北及港澳台地区）每日现有确诊病例人数（以下简称现有确诊病例）；

全国（不含湖北及港澳台地区）每日新增确诊病例人数（以下简称新增确诊病例）；

全国（不含湖北及港澳台地区）每日累计出院病例和累计死亡病例人数（以下合称治愈和死亡病例）。

2、数学符号定义

为方便描述，我们定义如下数学符号及含义：

3、疫情传播动力学模型

根据现有数据关系可以比较容易地建立IR模型：

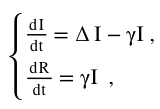
4、 模型参数辨识

模型中只有参数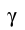是未知的并且随时间t变化，为了简化模型，我们假设参数 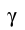为关于时间t的一元高次函数：

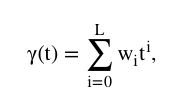
其中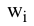，为待确定的未知参数，L为函数自变量t的最高次数。

经过这样的简化，疫情传播模型中就只剩下未知参数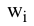 。我们构建如下参数辨识问题：

决策变量：未知参数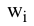 

目标函数：

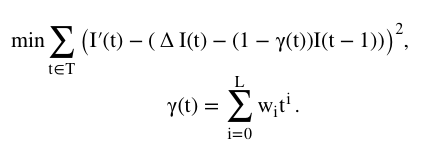
其中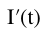，为第t天实际确诊病例数， T为疫情发展中的某段时间。

我们依然采用改进型的蝙蝠算法（BA）求解该问题的未知参数 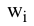。选取2020-02-01开始至2020-02-13这段时间的全国统计数据用于参数辨识，最终得到了一组最优解L=1, w= [0.01001219, 0.00274533]，计算过程略去。

5、 模型预测结果

将最优解导入模型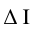，在未来一段时间的值用Holter-Winters算法预测值代替，经过数值计算得到如下图1所示结果。由该结果可知，2月14日至15日两天疫情各项统计指标的实际值与模型预测值误差不超过1.5%，最重要的信息是：新增确诊病例数将在2月19日左右降至个位数，确诊病例数峰值已过，即将进入快速减少阶段，预计在4月8日左右确诊病例降至个位数，4月中下旬疫情结束。考虑到大部分企业员工陆续返回公司上班，人员流动也会增加，疫情周期延长的风险仍然存在，后期疫情防控工作仍然需要重视，以防疫情反弹。

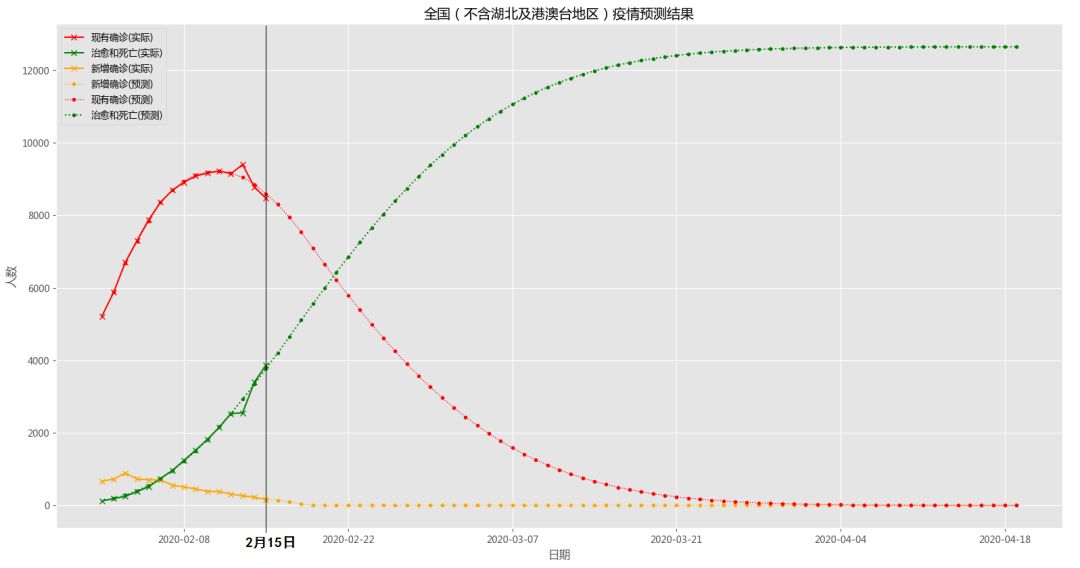
 图1 全国（不含湖北及港澳台地区）疫情预测结果

截至2020年2月16日24:00，全国（不含湖北及港澳台地区）新冠肺炎现有确诊病例数量峰值已经过去，即将进入加速减少阶段，预计4月中下旬疫情结束。继2月12日的拐点预测文章之后，湖北地区疫情数据发生了较大变化并且与全国其他地区的疫情差异较大。因此，本文利用湖北外的疫情数据再次从数学建模的角度分析全国（不含湖北及港澳台地区）疫情的发展趋势，为大家提前安排生产生活恢复工作提供一定的参考。相信在党中央的正确领导下和社会各界的努力下，新冠肺炎阻击战必胜。

疫情期间

免费使用Yonghong Desktop

前往下载使用